Problem 1: 

A roller-coaster car of mass 500 kg is at the top of a 30-meter hill. Calculate its potential energy at the top and its speed at the bottom, assuming no energy losses.

Problem 2:

A ball is thrown vertically upward with an initial speed of 15 m/s. Determine the maximum height it reaches.

Problem 3: 

A roller-coaster car starts from rest at the top of a hill. Assuming no friction or air resistance, what is the minimum height the hill must be so that the car reaches a speed of 25 m/s at the bottom?

Problem 4: 

A 2.0 kg model rocket is launched straight up. At its highest point, it reaches a height of 100 meters and momentarily comes to rest before descending. What is its speed just before impact? 

Problem 1

Find the gravitational force between two masses of 100 kg and 1000 kg separated by 10 meters.

Problem 2

Calculate the gravitational force between a 40 kg person and a 30 kg person standing 2 meters apart.

Problem 3

Determine the electrostatic force between charges of +2 μC and +4 μC placed 1 meter apart.

Problem 4

Calculate the electrostatic force between charges of +2 C and -1 C separated by 1 meter.

Problem 1:

Two carts are on a frictionless track.

Cart A has a mass of 2 kg and moves at 3 m/s toward Cart B, which has a mass of 1 kg and is initially at rest.

After the collision, the carts stick together.

What is their final velocity? 

Problem 2:

A 0.2 kg ball is thrown at 5 m/s toward a 0.8 kg person standing on a frictionless surface.

The person catches the ball.

What is their final velocity? 

Problem 3:

Two identical balls, each of mass 1 kg, are on a frictionless surface.

Ball A moves at 2 m/s toward Ball B, which is at rest.

They collide perfectly elastically. All energy is transferred.

What are their velocities after the collision? 

Problem 4:
A 3 kg cart moving at 4 m/s collides perfectly elastically (all energy is transferred) with a stationary 1 kg cart on a frictionless track.

What are their velocities after the collision? 

Problem 1: Constant Acceleration on a Ramp

A 5.0 kg box is released from rest at the top of a 30° frictionless incline that is 4.0 m long.

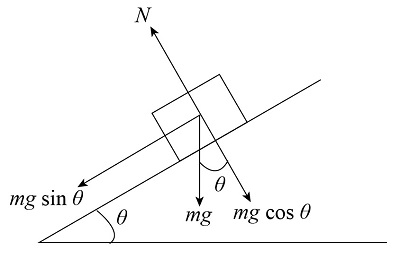
a) Draw a free-body diagram of the box.
b) Calculate the acceleration of the box down the ramp.
c) How long does it take for the box to reach the bottom of the ramp?
d) What is the box’s speed at the bottom of the ramp?

Problem 2: Ramp Acceleration and Speed

A 3.0 kg block is released from rest at the top of a frictionless 35° incline that is 2.5 meters long.

a) Draw a free-body diagram of the block.
b) Calculate the acceleration of the block down the ramp.
c) How long does it take for the block to reach the bottom?
d) What is the block’s speed at the bottom?

Problem 3: Heavier Object, Shallower Ramp

A 12.0 kg crate is released from rest at the top of a 20° incline. The ramp is frictionless and 6.0 meters long.

a) Draw a free-body diagram of the crate.
b) Determine the crate’s acceleration down the ramp.
c) Calculate how long it takes the crate to slide to the bottom.
d) What is the final speed of the crate when it reaches the bottom?

Problem 4: Identifying Unknown Ramp Length

A 4.0 kg object slides down a frictionless incline angled at 40°. It accelerates at 6.3 m/s² and takes 1.5 seconds to reach the bottom.

a) Draw a free-body diagram of the object.
b) Confirm the acceleration using Newton’s Second Law.
c) Calculate how far the object traveled along the ramp.
d) Determine the final velocity of the object at the bottom.

Key: 1) 6.26 m/s, 2) 5.30 m/s, 3) 6.34 m/s, 4) 9.45 m/s